Areas of Parallelograms and Triangles Exercise 9.2
ncert class 9 maths chapter 9 solution, areas of parallelograms and triangles Exercise 9.2 involve complete answers for each question in the exercise 9.2. The solutions provide students a strategic methods to prepare for their exam. Class 9 Maths Chapter 9 areas of parallelograms and triangles exercise 9.2 questions and answers helps students to perform better in exam and it will clear doubts definitely. Students will find it extremely easy to understand the questions and learn solving the problems.NCERT Solutions for Class 9 Maths Chapter 9 areas of parallelograms and triangles prepared by www.mathematicsandinformationtechnology.com team in very delicate, easy and creative way.
1. In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
Solution 1:
In parallelogram ABCD, CD = AB = 16 cm [Opposite sides of a parallelogram are equal]
Area of a parallelogram = Base × Corresponding altitude
Area of parallelogram ABCD = CD × AE = AD × CF
16 cm × 8 cm = AD × 10 cm
Thus, the length of AD is 12.8 cm.
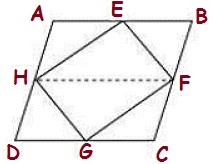
2. If E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that
ar (EFGH) =1/2 ar (ABCD)
Let us join HF.
In
parallelogram ABCD,
AD = BC and AD
|| BC (Opposite sides of a parallelogram are equal and parallel)
AB = CD
(Opposite sides of a parallelogram are equal)
½ AD=½ BC and AH
|| BF
⇒AH = BF and AH || BF (
H and F are
the mid-points of AD and BC)
Therefore,
ABFH is a parallelogram.
Since ΔHEF and
parallelogram ABFH are on the same base HF and between the same parallel lines
AB and HF,
∴ Area (ΔHEF) =½ Area (ABFH) ... (1)
Similarly, it
can be proved that
Area (ΔHGF) =½
Area (HDCF) ... (2)
On adding
Equations (1) and (2), we obtain
Area (ΔHEF) +
Area (ΔHGF) =½ Area (ABFH) +½ Area (HDCF)
=½ [Area
(ABFH) + Area (HDCF)]
Area(EFGH) =½Area
(ABCD)
3. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
It can be observed that ΔBQC and parallelogram ABCD lie on the same base BC and these are between the same parallel lines AD and BC.
∴ Area (ΔBQC) =½ Area (ABCD) ... (1)
Similarly,
ΔAPB and parallelogram ABCD lie on the same base AB and between the same
parallel lines AB and DC.
∴ Area (ΔAPB) =½ Area (ABCD) ... (2)
From Equations
(1) and (2), we obtain
Area (ΔBQC) =
Area (ΔAPB)
4. In Fig, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) =1/2 ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint : Through P, draw a line parallel to AB.]
(i)Let us draw a line segment EF, passing through point P and parallel to line segment AB.
In parallelogram ABCD,
AB || EF (By construction) ... (1)
ABCD is a parallelogram.
∴ AD || BC (Opposite sides of a parallelogram)
⇒ AE || BF ... (2)
From Equations (1) and (2), we obtain
AB || EF and AE || BF
Therefore, quadrilateral ABFE is a parallelogram.
It can be observed that ΔAPB and parallelogram ABFE are lying on the same base AB and between the same parallel lines AB and EF.
∴ Area (ΔAPB) =½ Area (ABFE) ... (3)
Similarly, for ΔPCD and parallelogram EFCD,
Area (ΔPCD) =½ Area (EFCD) ... (4)
Adding Equations (3) and (4), we obtain
Area (ΔAPB) + Area (ΔPCD) =½[Area (ABFE) + Area (EFCD)]
Area (ΔAPB) + Area (ΔPCD) =½ Area (ABCD) ... (5)
ii) Let us draw a line segment MN, passing through point P and parallel to line segment AD.
In parallelogram ABCD,
MN || AD (By construction) ... (6)
ABCD is a parallelogram.
∴ AB || DC (Opposite sides of a parallelogram)
⇒ AM || DN ... (7)
From Equations (6) and (7), we obtain
MN || AD and AM || DN
Therefore, quadrilateral AMND is a parallelogram.
It can be observed that ΔAPD and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.
∴ Area (ΔAPD) =½ Area (AMND) ... (8)
Similarly, for ΔPCB and parallelogram MNCB,
Area (ΔPCB) =½ Area (MNCB) ... (9)
Adding Equations (8) and (9), we obtain
Area (ΔAPD) + Area (ΔPCB) =½ [Area (AMND) + Area (MNCB)]
Area (ΔAPD) + Area (ΔPCB) = ½Area (ABCD) ... (10)
On comparing Equations (5) and (10), we obtain
Area (ΔAPD) + Area (ΔPBC) = Area (ΔAPB) + Area (ΔPCD)
5. In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AX S) =1/2 ar (PQRS)
Solution 5:
(i)It can be observed that parallelogram PQRS and ABRS lie on the same base SR and also,these lie in between the same parallel lines SR and PB.
∴ Area (PQRS) = Area (ABRS) ... (1)
(ii)Consider ΔAXS and parallelogram ABRS.
As these lie on the same base and are between the same parallel lines AS and BR,
∴ Area (ΔAXS) =½ Area (ABRS) ... (2)
From Equations (1) and (2), we obtain
Area (ΔAXS) =½ Area (PQRS)
6. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Solution 6:
From the figure, it can be observed that point A divides the field into three parts.
These parts are triangular in shape − ΔPSA, ΔPAQ, and ΔQRA
Area of ΔPSA + Area of ΔPAQ + Area of ΔQRA = Area of parallelogram PQRS ... (1)
We know that if a parallelogram and a triangle are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram.
∴ Area (ΔPAQ) =½ Area (PQRS) ... (2)
From Equations (1) and (2), we obtain
Area (ΔPSA) + Area (ΔQRA) =½Area (PQRS) ... (3)
Clearly, it can be observed that the farmer must sow wheat in triangular part PAQ and pulses in other two triangular parts PSA and QRA or wheat in triangular parts PSA and QRA and pulses in triangular parts PAQ.