ex 1.2 class 9

ex 1.2 class 9 involve complete  answers for each question in the exercise 1.2. The solutions provide students a strategic methods  to prepare for their exam. ex 1.2 class 9 questions and answers helps students to perform better in exam and it will  clear doubts definitely. Students will find it extremely easy to understand the questions and learn solving the problems.ex 1.2 class 9 prepared by www.mathematicsandinformationtechnology.com team in very delicate, easy and creative way. 

Question 1:

State whether the following statements are true or false.

(i) Every irrational number is a real number.

(ii) Every point on the number line is of the form √m , where m is a natural number.

(iii) Every real number is an irrational number.

Solution 1:

i).Yes

ii).No

iii).No

Question 2:

Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Solution 2:

Square root of every positive integer will not yield an integer.

(Eg: \(\sqrt{2},\sqrt{3},\sqrt{6}…)\) which are called irrational numbers. But \(\sqrt{4}\) is \(2\), which is an integer.

Therefore, we conclude that square root of every positive integer is not an irrational number.

Question 3:

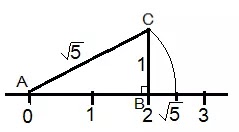
Show how √5 can be represented on the number line.

Solution 3:

We need to draw a line segment \(AB\) of \(2\) unit on the number line.

Then draw a perpendicular line segment \(BC\) at \(B\) of \(1\) units.

Then join the points \(C\) and \(A\), to form a line segment \(AC\).

According to Pythagoras Theorem

\(AC^2 = AB^2 +BC^2\)

\(AC^2 = 2^2 + 1^2\)

\(AC^2 = 4 + 1 = 5\)

\(AC = \sqrt{5}\)

Then draw the arc ACD, to get the number \( \sqrt{5}\) on the number line.